¿Qué relación guardan estos dos majestuosos organismos?

El General Sherman (una secuoya del Sequoia National Park ) tiene 11 metros de diámetro en su base. Montaje del autor a partir de fotografías de Wikimedia Commons)

Panthera tigris tigris (wikimedia commons)
Aunque a simple vista pueda parecer extraño, uno de los vínculos que relacionan estos dos seres vivos puede ser el metabolismo, la red integrada de reacciones bioquímicas que mantienen la vida de un organismo. Nos referimos a los diferentes mecanismos que emplean los animales, las plantas, las bacterias etc., para obtener y procesar la energía necesaria para realizar las funciones vitales y aumentar de tamaño. El metabolismo de un árbol y un animal es diferente, pero en esencia no se trata más que de un intercambio de materia y energía con el medio.
Los mayores organismos, los que poseen mayor masa y una vida más larga que han existido nunca no fueron los dinosaurios ni las ballenas, ni siquiera son animales sino árboles. Las secoyas gigantes (Sequoiadendron giganteum) como el General Sherman de la imagen superior, llegan a elevarse por encima de los 110 metros y alcanzan perímetros de hasta 30 metros. Las más antiguas superan los 4.000 años de vida (es decir, estaban creciendo al mismo tiempo que se construían las pirámides del Egipto faraónico).
Podemos imaginar la evolución de estos enormes árboles como una carrera de armamentos en la que cada uno lucha con sus vecinos para ver quién sobresale por encima de los demás. Los árboles crecen a lo alto y desarrollan copas anchas porque compiten con otros por la luz y el agua y, a diferencia de lo que ocurre con los mamíferos terrestres o con las aves, siguen creciendo una vez alcanzan la madurez sexual. Dado que la búsqueda de recursos supone un imperativo constante, con el tiempo pueden llegar a adquirir un tamaño descomunal.
En el caso de las secuoyas gigantes, son tan grandes por su extraordinaria longevidad, y son tan longevas porque han sobrevivido a todas las amenazas que podrían haber acabado con ellas: su enorme fortaleza impide que el viento las tumbe, los ácidos tánicos y otras sustancias químicas que producen las protegen de los hongos, y su gruesa corteza es ignífuga. En definitiva, la recompensa en esta carrera evolutiva supone, para el árbol vencedor, mayor éxito reproductor y por tanto, la posibilidad de transmitir sus genes a través de sus descendientes, altos también.
Por otro lado, el tigre de Bengala (Panthera tigris tigris), es una subespecie de tigre que habita en varios lugares de la India y el sudeste asiático. Es la más numerosa y la de mayor tamaño: la longitud total de los machos oscila entre los 270 y 310 centímetros, con un peso promedio de 221,2 kilogramos.
Como todos los tigres, se trata de animales solitarios con una alimentación basada en una dieta carnívora. Según algunos estudios, tan solo el 5% de los ataques del tigre acaban en éxito y da muerte, como promedio, a entre 40 y 50 presas cada año, lo que equivale a una cada ocho días (debemos tener presente que las presas alcanzan un amplio rango de tamaños, algunas tan grandes como crías de elefantes). La esperanza de vida para los tigres de Bengala machos es de entre 10 y 12 años, aunque hay animales que han llegado a doblar esa cifra en cautividad.
Podemos pensar que el árbol tiene la tarea más fácil a la hora de obtener nutrientes: se limita a obtener agua a través de sus raíces y a convertir la luz solar en energía para crecer en un cuerpo más o menos estable. Para hacerlo de la forma más eficiente posible, el árbol tiene una forma de ramificación con muchas superficies verdes, tallos y hojas, donde se realiza la fotosíntesis, y una raíz que crece en dirección inversa y se hunde en la tierra para absorber agua y sales minerales.
Por su parte, el tigre necesita alimentarse cazando presas con las que obtener la energía para mantener sus células en funcionamiento. Su ventaja respecto al árbol reside en que puede moverse, aunque ese movimiento, y el resto de funciones metabólicas, produce un calor que se origina de manera constante debido a los procesos bioquímicos que acompañan la formación de tejidos, la conversión de energía y el trabajo muscular (entre otros). Dado el enorme esfuerzo que supone la caza, tiene que encontrar una manera de deshacerse de ese exceso de calor corporal (que podría llevarle a la muerte).
La manera obvia de hacerlo sería enfriar su superficie (su piel) pero como el tamaño de su piel es proporcionalmente menor que su masa, este mecanismo por sí solo no es suficiente. Por ejemplo, y al contrario que la piel del tigre, el radiador de un coche sí está diseñado expresamente para maximizar el tamaño de su superficie en contacto con el aire a través de un número significativo de cámaras y pliegues.
En definitiva, a medida que los animales se hacen más grandes en tamaño, su metabolismo debe aumentar a un ritmo más lento que su volumen, o no serían capaces de deshacerse del exceso de calor.
Con estos antecedentes, vamos a analizar si es posible que el metabolismo guarde algún tipo de relación con la masa de estos organismos, independientemente de la forma, la fisiología y la historia evolutiva de árboles y animales.
Forma, función y evolución de los organismos vivos

Las proporciones del hombre. Cuaderno de notas. Alberto Durero (fuente)
Hace unas semanas se publicó en la revista PNAS un artículo que me llamó la atención. Lo incluí en el resumen semanal de noticias científicas que publico todos los lunes esperando tener un rato libre para leerlo con calma y estudiarlo en profundidad. En esta anotación vamos a analizar sus conclusiones. Para facilitar la lectura he dividido el texto en dos partes: en esta primera vamos a explicar el objetivo de la investigación y algunos conceptos imprescindibles para seguir sus argumentos, mientras que en la segunda parte entraremos de lleno en las conclusiones del estudio.
Bajo el título “Forma, función y evolución de los organismos vivos” (Form, function, and evolution of living organisms), el equipo de investigadores formado por dos físicos (Jayanth Banavarr y Amos Maritan), un botánico (Todd Cooke) y un hidrólogo (Andrea Rinaldo) sugiere que las plantas y los animales llegaron a soluciones similares (evolutivamente hablando) para resolver el problema del uso eficiente de la energía, y que evolucionaron en respuesta a los mismos principios físicos.
Incluso bajo un examen superficial, está claro que la forma de los animales y las plantas es distinta si tenemos en cuenta la distribución de la masa sobre el volumen. Los animales son capaces de moverse y mantienen una cierta homogeneidad en la distribución de su masa corporal. Por el contrario, las plantas permanecen inmóviles y presentan una geometría heterogénea donde la masa se concentra en el tallo y las ramas en lugar de en las hojas. Los autores de este estudio tratan de ofrecer, al tratar la física fundamental que subyace a la relación entre la forma y la fisiología de plantas y animales, una explicación acerca de cómo han evolucionado de forma independiente para lograr eficiencias energéticas equivalentes.
Proporciones y tamaño *
No creo que nadie que se haya parado a observar las maravillas del mundo animal y vegetal permanezca indiferente ante la enorme diversidad de formas y tamaños que pueden llegar a presentar. Recapacitar sobre esta variedad, fruto de la evolución de nuevas especies y el tamiz que las filtra ―la selección natural― nos debería llevar a plantearnos una serie de preguntas muy interesantes:
¿Por qué hay ardillas voladoras y no caballos que trepen por los árboles y planeen con membranas de piel tirante entre sus patas? ¿Por qué una hormiga es capaz de levantar diez veces su propio peso, mientras que a nosotros nos cuesta sostener y transportar un peso superior al nuestro? ¿Por qué los mamíferos más pequeños, como la musaraña etrusca (Suncus etruscus), de unos cuatro centímetros de longitud; y el menor de los pájaros, el colibrí zunzuncito (Mellisuga helenae), de unos cinco centímetros de largo, vienen a coincidir en peso (unos tres gramos)? ¿Por qué los menores insectos y arácnidos son todavía más pequeños?
Estas y otras muchas preguntas han sido objeto de debate entre zoólogos, físicos, botánicos, biólogos y otros muchos científicos desde hace décadas, en un intento de comprender la posible relación entre el tamaño, la forma y el desarrollo de los diferentes organismos. Como resultado tenemos una serie de hipótesis de trabajo que se someten constantemente a revisión para afinar al máximo sus predicciones.
Para mí, la mejor representación gráfica de esta enorme variedad la encontramos en la obra The Science of Life, publicada en tres volúmenes entre 1929 y 1930 por Herbert George Wells (el escritor de “La Guerra de los Mundos”), Julian Huxley y el zoólogo George P. Wells (hijo del primero). Esta lámina proporciona una excelente imagen de los tamaños extremos en los que nos movemos los seres vivos (la imagen 26 corresponde a los primeros 32 metros de una secuoya gigante):

Hay muchos casos en la naturaleza en los que el tamaño parece imponer restricciones específicas a la forma. Si una planta o un animal es grande, las restricciones físicas que actúan sobre sus proporciones son diferentes de las que operan en el caso contrario. Expuesto de otro modo, hay formas que, desde un punto de vista físico, es imposible que un organismo grande pueda adoptar; y otras no menos prohibidas para los pequeños. Y este argumento actúa en ambas direcciones ya que la forma también impone ciertas condiciones al tamaño. El ejemplo más claro lo tenemos en las aves. Aunque un ave vuele, su peso, que guarda una relación directa con su tamaño, debe permanecer dentro de un límite estricto (a nadie le extraña que las aves con cuerpos muy grandes, como las avestruces, hayan perdido la facultad de volar).
Una vez se comprendió que los cambios de tamaño solían ir acompañados de cambios en la forma, se planteó la necesidad de contar con un método para medirlos. El primer paso en ese sentido fue idear un modo de representar gráficamente los cambios de las proporciones, con la esperanza de que si se hacía correctamente conduciría a identificar un método para su medición.
En este sentido, los dibujos de Leonardo da Vinci y Alberto Durero sirvieron de inspiración para el biólogo y matemático escocés D´Arcy Thompson quien, en 1917, revolucionó la disciplina con el libro On growth and form (Sobre el crecimiento y la forma), donde sugería un ingenioso método para relacionar ambas variables: lo llamó transformación cartesiana y lo aplicó para medir las diferencias en las proporciones de tamaño entre especies emparentadas. Sin embargo, como muchos han apuntado desde entonces, se trata de un método difícil de utilizar analíticamente por su escasa precisión y porque hace representaciones bidimensionales de objetos tridimensionales. Y quizás lo más importante, visualiza muchos cambios a la vez, lo que dificulta enormemente asignar valores numéricos a las líneas cambiantes de la trama.

Transformación cartesiana de D´Arcy Thompson ( fuente: On growth and form )
Alometría
Un enfoque más sencillo (y más útil) comparado con las complejidades matemáticas de las transformaciones cartesianas de Thompson, fue el desarrollado por Julian Huxley (en Problems of relative growth – se puede descargar en formato pdf aquí), al que hizo fundamentales contribuciones Georges Teissier (en Recherches morphologiques et physiologiques sur la croissance des insectes – se puede descargar en formato pdf aquí) Este método se limita a cotejar la relación entre dos parámetros, dejando de lado todas las complejidades y sutilezas de los cambios de forma.
En 1936 ambos científicos acuñaron el término “alometría” para referirse a este método en un artículo conjunto publicado en inglés (en Nature) y francés (Comptes rendus de la Société de biologie) con la intención manifiesta de desterrar la confusión existente en el campo del crecimiento relativo. Aunque la definición moderna del término es aún objeto de controversia, podemos entender por alometría los cambios en las dimensiones relativas de las partes de un organismo que se correlacionan con cambios en el tamaño global; o, dicho de forma más concisa, la relación que existe entre los cambios en la forma y el tamaño global.
Junto a la adopción de un término unívoco, acordaron también el empleo de los símbolos de la fórmula algebraica:
![]() fórmula que constituye una ley de potencias y que también puede expresarse como una expresión logarítmica:
fórmula que constituye una ley de potencias y que también puede expresarse como una expresión logarítmica:
![]()
(donde log significa “logaritmo en base 10″, un exponente del número 10; y donde α y b son constantes). Si α es igual a cero, y siempre es igual a la constante b, cualquiera que sea el valor de x (recordemos que un número elevado a 0 siempre es igual a 1).
Quizás comprendamos mejor el uso de esta fórmula con un ejemplo sencillo. Supongamos que tenemos dos series de mediciones como la longitud de los brazos y la altura de un conjunto de hombres adultos. Si asignamos la variable y para la longitud de los brazos, y la x para la altura, la ecuación se ajusta bien a la realidad si hiciéramos que α fuera igual a 1 ya que, en este caso, la longitud de los brazos sería directamente proporcional a la altura. Y esta es precisamente la característica que presenta la anatomía humana, algo que conocemos bien desde que Leonardo da Vinci la representó en su famoso dibujo “El hombre de Vitrubio”. Vemos por tanto que el punto clave está en determinar el valor de α, valor que podemos obtener a partir de observaciones cuidadosas y de la representación gráfica de esos datos observacionales.
Esto es así porque las fórmulas que siguen la ley de potencias del tipo descrito más arriba dan líneas rectas al representarlas en papel logarítmico (ver representación logarítmica en wikipedia) y también porque la pendiente de esa representación es el exponente α de la ley de potencias.
Si los datos puntuales que describen un experimento, o un conjunto de observaciones, dibujan una línea recta al representarlos en papel logarítmico, podemos estar seguros de que la fórmula que analizamos describe la relación entre x e y. Además, como hemos dicho, el exponente α y la constante b pueden leerse directamente a partir de la pendiente de la curva logarítmica y del valor de y cuando hacemos que x sea igual a 1. Expliquemos esto antes de continuar:
Las representaciones logarítmicas, a diferencia de las gráficas cartesianas, permiten incluir un enorme rango de valores en un mismo gráfico. Para hacerlo, el gráfico logarítmico disminuye el espacio entre los números a medida que éstos son más grandes y dilata ese espacio cuando son pequeños. Curiosamente, actuamos de la misma forma cuando mantenemos cerca de nuestros ojos algo pequeño, y nos alejamos cuando queremos tener una visión completa de algo más grande.
Para construir esta escala logarítmica se emplea usualmente la base 10. Así, la distancia entre 10 y 100 es la misma que entre 1 y 10, y la marca del 10 dista del 20,lo mismo que la del 1 de la del 2, como podemos ver en esta figura:

Supongamos que tenemos dos medidas relacionadas con la dimensión de un cráneo: una la consignaremos bajo el valor de x, y la otra bajo el valor de y. Al examinar un total de 18 cráneos de diferentes tamaños, incorporamos sus medidas en una tabla como ésta:
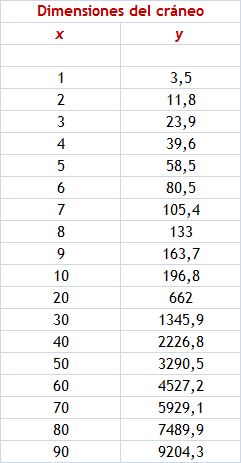
Vamos a representar y en función de x en una gráfica logarítmica (colocando en el eje horizontal o de las abscisas las mediciones de x, y en el eje vertical o de las ordenadas las mediciones de y). Vemos como la representación de los datos dibuja una línea perfectamente recta (algo que en la práctica no suele ocurrir con tanta precisión)
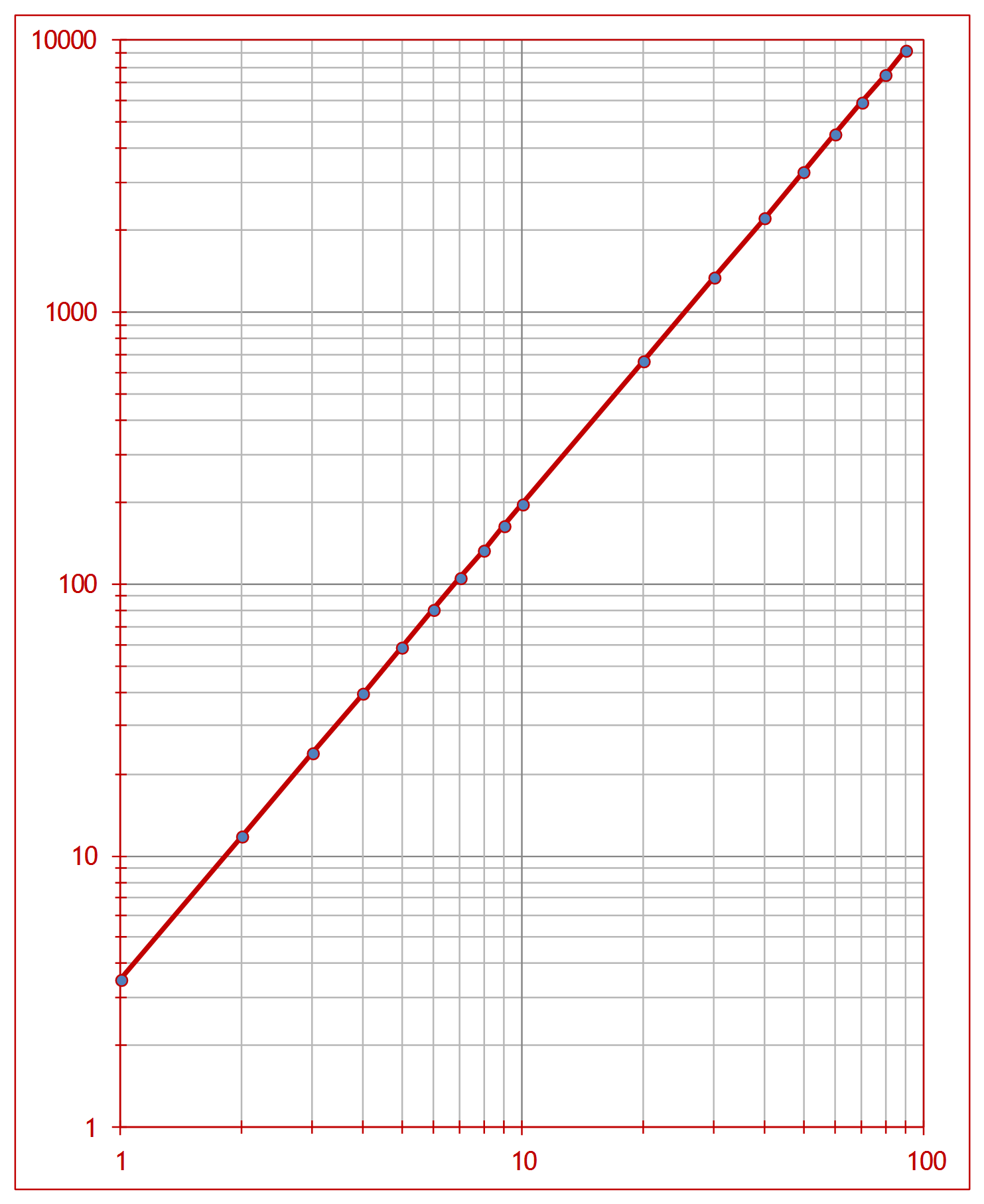
Representación logarítmica (realizado con el programa Excel©)
Ahora ya podemos obtener la pendiente de la representación directamente del gráfico ―que recordemos es igual al exponente α de la fórmula descrita más arriba―. Para ello medimos, con una regla ordinaria, el incremento en la distancia vertical entre dos puntos cualesquiera de la línea (1) y dividimos ese resultado por el incremento en la distancia horizontal entre dichos puntos (2), medida con la misma regla. Utilizando este procedimiento, calculamos que en nuestro caso concreto, la pendiente es de 1,75.

Tomando en consideración que, según las mediciones que habíamos registrado en la tabla, el valor de y para x=1 es de 3,5 no tenemos más que despejar para obtener el valor de b que arroja el siguiente resultado

Cuando la ecuación ![]() se usa para relacionar una dimensión x, con otra y en una serie de organismos de diferentes tamaños, se denomina formula alométrica. Es importante que tengamos presente que esta relación alométrica es meramente descriptiva y no ofrece una explicación de por qué se dan esas proporciones.
se usa para relacionar una dimensión x, con otra y en una serie de organismos de diferentes tamaños, se denomina formula alométrica. Es importante que tengamos presente que esta relación alométrica es meramente descriptiva y no ofrece una explicación de por qué se dan esas proporciones.
La forma en que se llegó esta relación es muy ilustrativa al respecto. Huxley y otros tomaron gran cantidad de medidas de diferentes partes de animales y plantas para intentar encontrar una relación entre las mismas. En un número sorprendente de organismos, al representar los datos en papel logarítmico, aparecía una línea recta como la que hemos visto más arriba.
Sin embargo, no todas las medidas proporcionaron líneas perfectamente rectas. En algunos casos aparecían dos o más líneas rectas o, en otros, la línea se curvaba ligeramente. El primer caso es señal de un súbito cambio en el valor de α, que puede significar la transición de una etapa de desarrollo a otra; por ejemplo, antes y después de alcanzar la madurez sexual. En otros casos, el valor de α cambia de modo continuo dando una línea curva. En estas situaciones resulta de poca utilidad el análisis alométrico.
En definitiva, lo que demuestra la fórmula alométrica es la existencia de un cambio de proporciones con el cambio de tamaño. Ahora bien, la pregunta importante que debemos plantearnos es si se puede aplicar este método de análisis a organismos de diferentes especies y tan distintos entre sí como los animales y las plantas, así como qué relación guarda la masa con la superficie, el volumen y el metabolismo de un organismo.
Isometría
La isometría, o semejanza geométrica, se da cuando el exponente α de la ecuación alométrica descrita más arriba es igual a 1. Es decir, son los casos en que si x duplica su longitud, y hace lo propio, o lo que es lo mismo, cuando las proporciones permanecen constantes, sin variaciones con el cambio de tamaño (para entender fácilmente este concepto solo tenemos que pensar en las ampliaciones fotográficas que permiten obtener imágenes de diferentes tamaños pero con idénticas proporciones). Cuando realizamos comparaciones entre individuos de diferentes tamaños dentro de una misma especie encontramos generalmente este tipo de isometría.
Según lo estipulado por la isometría, el área debe ser proporcional al cuadrado de la longitud del organismo. De esta forma, para animales geométricamente semejantes y de la misma densidad, la masa corporal, m, es proporcional al cubo de la longitud del cuerpo, de ahí que la longitud sea proporcional a la raíz cúbica de la masa corporal. Con estos datos se sigue que las áreas deben seguir las mismas proporciones que las masas corporales elevadas a la potencia 2/3. Como han corroborado numerosos estudios, se ha constatado en muchas especies que las áreas de superficie resultan ser proporcionales a la potencia 2/3 de la masa corporal.

Como ya hemos apuntado más arriba, al comparar animales o plantas terrestres de tamaños muy diferentes las proporciones cambian con el tamaño y son alométricas. Por ello la isometría rige sólo para comparaciones hechas dentro de un rango limitado de tamaños, en el seno de la misma especie o en otras circunstancias particulares.
Algunas pinceladas más sobre el metabolismo
Ahora que hemos analizado las proporciones, el cambio de tamaño y de forma, concluimos la primera parte de esta anotación exponiendo algunos conceptos relacionados con el metabolismo y la generación de calor.
Como ya hemos señalado, una gran parte de la energía química absorbida por el organismo se libera en forma de calor. En la tasa de intercambio de calor intervienen tres factores esenciales: la tasa de generación de calor a través del metabolismo, la tasa de ganancia de calor debida a las condiciones ambientales y la tasa de pérdida de calor al medio ambiente. Así, los organismos pueden perder o ganar calor a través de diferentes procesos físicos:
- conducción: es la transferencia de calor entre sustancias u objetos en contacto. Si la temperatura del medio circundante es inferior a la del cuerpo, éste experimenta una pérdida de calor; mientras que si la temperatura del medio es superior, la transferencia se invierte (ganancia de calor).
- convección: es la transferencia de calor contenido en una masa de fluido (ya sea gas o líquido) por el movimiento de la masa del mismo. Este proceso, que ocurre en todo fluido, hace que el aire caliente ascienda y sea reemplazado por aire más frío, creando una corriente térmica.
- radiación: transferencia a través de la radiación electromagnética sin contacto directo.
- evaporación: el cambio de estado de líquido a gas requiere gran cantidad de calor en el caso del agua. Muchos animales disipan calor permitiendo que se evapore agua en su superficie corporal (sudoración).
El tercer factor en el intercambio de calor es la tasa metabólica. Para su análisis se tiene en cuenta la tasa metabólica basal: la tasa de consumo de energía en seres homeotermos (organismos que mantienen su temperatura corporal dentro de unos límites, independientemente de la temperatura ambiental) medida en condiciones de reposo, ayuno y temperatura ambiental termoneutra (rango de temperatura ambiental en el que un organismo no necesita activar procesos de eliminación o generación de calor para mantener su temperatura corporal constante).
En los estudios de fisiología comparada se ha podido establecer que la masa de los animales influye de manera muy importante en su tasa metabólica. Aunque la tasa metabólica aumenta uniformemente con la masa, el incremento no es proporcional al mismo. Los animales de mayor tamaño consumen proporcionalmente menos energía que un animal de tamaño pequeño.
La explicación de esta relación viene dada por la ley de la superficie. Los mamíferos y las aves tienden a perder calor de manera más o menos constante porque mantienen temperaturas que suelen estar por encima de la temperatura ambiental. Y, como ya dijimos al comienzo, a medida que los animales se hacen más grandes en tamaño, su metabolismo debe aumentar a un ritmo más lento que su volumen, o no serían capaces de deshacerse del exceso de calor.
Con todo lo expuesto hasta ahora estamos en disposición de analizar las conclusiones del estudio publicado en PNAS, cosa que haremos en la segunda parte. No se la pierdan.
Esta anotación participa en la XXIX Edición del Carnaval de Biología que organiza ::ZTFNews

Artículo principal:
Banavar JR, Cooke TJ, Rinaldo A, & Maritan A (2014). Form, function, and evolution of living organisms. Proceedings of the National Academy of Sciences of the United States of America, 111 (9), 3332-7 PMID: 24550479
(Ver artículo completo aquí)
Otras referencias:
McMahon, T. A. y Bonner, J. T. (1986), Tamaño y vida. Barcelona: Prensa Científica, 255 p.
Huxley, J. S. y Teissier, G. (1936a), “Terminology of relative growth”. Nature, vol. 137, núm. 3471, p. 780-781.
Huxley, J. S. y Teissier, G. (1936b). “Terminologie et notation dans la description de la croissance relative”. Comptes rendus de la Société de biologie, tomo 121, p. 934–937
Gayon, J. (2000), “History of the concept of allometry“. American Zoologist, vol. 40, núm. 5, p. 748-758.
Gayon, J. (2000), “De la croissance relative à l’allométrie (1918-1936)“. Revue d’histoire des sciences, vol. 53, núms. 3-4, p. 475-498





Pingback: Los números de la biología (y II) | Afán por saber
Pingback: Resumen de la XXIX edición del Carnaval de Biología | :: ZTFNews.org
Pingback: Participaciones en la XXIX Edición del Carnaval de Biología | :: ZTFNews.org
Pingback: Los números de la biología (I) | …
Pingback: Los números de la biología (I) | …